圖形計(jì)數(shù)專題,深度探索與策略解析
在當(dāng)今數(shù)字化時(shí)代,圖形計(jì)數(shù)不僅是數(shù)學(xué)領(lǐng)域的一個(gè)重要分支,而且在計(jì)算機(jī)科學(xué)、工程設(shè)計(jì)和許多其他領(lǐng)域也發(fā)揮著關(guān)鍵作用,本文將圍繞“圖形計(jì)數(shù)專題”展開(kāi)討論,介紹圖形計(jì)數(shù)的概念、應(yīng)用、方法和策略。
什么是圖形計(jì)數(shù)
圖形計(jì)數(shù)是數(shù)學(xué)中的一個(gè)重要概念,涉及對(duì)圖形的元素進(jìn)行計(jì)數(shù),如頂點(diǎn)、邊、面等,通過(guò)對(duì)圖形的元素進(jìn)行計(jì)數(shù),我們可以更深入地理解圖形的性質(zhì)和結(jié)構(gòu),圖形計(jì)數(shù)在計(jì)算機(jī)科學(xué)、工程設(shè)計(jì)和許多其他領(lǐng)域也具有廣泛應(yīng)用。
圖形計(jì)數(shù)專題的應(yīng)用
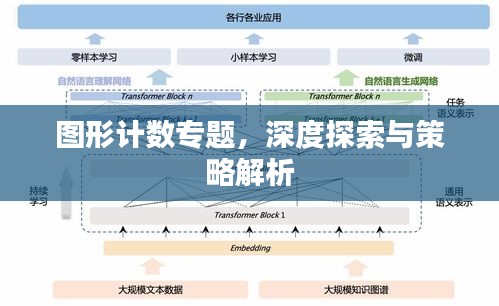
1、計(jì)算機(jī)科學(xué):在計(jì)算機(jī)圖形學(xué)領(lǐng)域,圖形計(jì)數(shù)用于計(jì)算圖形的復(fù)雜性、優(yōu)化算法和渲染技術(shù),數(shù)據(jù)庫(kù)管理系統(tǒng)也利用圖形計(jì)數(shù)技術(shù)來(lái)優(yōu)化數(shù)據(jù)查詢和存儲(chǔ)。
2、工程設(shè)計(jì):在建筑工程、機(jī)械工程等領(lǐng)域,圖形計(jì)數(shù)有助于設(shè)計(jì)師分析結(jié)構(gòu)的穩(wěn)定性和強(qiáng)度,橋梁和建筑物的支撐結(jié)構(gòu)需要進(jìn)行復(fù)雜的圖形計(jì)數(shù)分析以確保其安全性。
3、生物學(xué)和醫(yī)學(xué):生物學(xué)家和醫(yī)學(xué)研究人員利用圖形計(jì)數(shù)技術(shù)來(lái)研究細(xì)胞結(jié)構(gòu)、神經(jīng)網(wǎng)絡(luò)和蛋白質(zhì)相互作用等復(fù)雜系統(tǒng)。
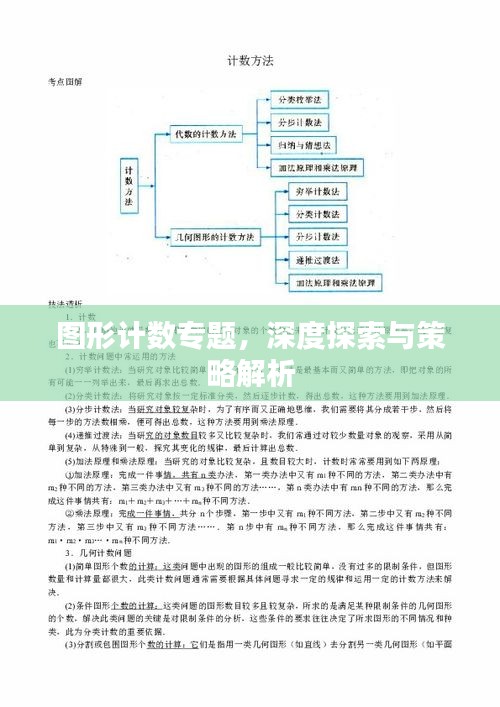
圖形計(jì)數(shù)的策略和方法
1、系統(tǒng)法:系統(tǒng)法是一種基本的圖形計(jì)數(shù)策略,通過(guò)將圖形分解為更簡(jiǎn)單的子圖來(lái)簡(jiǎn)化問(wèn)題,我們可以分別計(jì)算子圖的元素?cái)?shù)量,最后將結(jié)果相加得到整個(gè)圖形的元素?cái)?shù)量。
2、排除法:在某些情況下,我們可能需要從總數(shù)中排除一些元素以得到最終結(jié)果,排除法是一種有效的策略,可以幫助我們處理這種情況,通過(guò)識(shí)別并排除不需要計(jì)數(shù)的元素,我們可以更準(zhǔn)確地計(jì)算圖形的元素?cái)?shù)量。
3、遞歸法:遞歸法是一種適用于復(fù)雜圖形的計(jì)數(shù)策略,通過(guò)將圖形分解為相似的較小部分,我們可以遞歸地計(jì)算每個(gè)部分的元素?cái)?shù)量,然后將結(jié)果組合起來(lái)得到整個(gè)圖形的元素?cái)?shù)量,這種方法在處理具有相似結(jié)構(gòu)和重復(fù)模式的圖形時(shí)特別有效。
案例分析與實(shí)踐應(yīng)用
為了更好地理解圖形計(jì)數(shù)專題,我們可以通過(guò)一些實(shí)際案例進(jìn)行分析和實(shí)踐,我們可以研究一個(gè)社交網(wǎng)絡(luò)的圖結(jié)構(gòu),計(jì)算其頂點(diǎn)(用戶)和邊(連接)的數(shù)量,以了解網(wǎng)絡(luò)的基本屬性,我們還可以分析一個(gè)建筑物的支撐結(jié)構(gòu)圖,計(jì)算其各種元素的數(shù)量以評(píng)估結(jié)構(gòu)的穩(wěn)定性,這些案例不僅有助于我們理解圖形計(jì)數(shù)的實(shí)際應(yīng)用,還可以提高我們的問(wèn)題解決能力。
圖形計(jì)數(shù)專題是一個(gè)涵蓋廣泛領(lǐng)域的課題,具有許多實(shí)際應(yīng)用,通過(guò)掌握不同的圖形計(jì)數(shù)策略和方法,我們可以更好地理解和分析圖形的性質(zhì)和結(jié)構(gòu),通過(guò)實(shí)踐應(yīng)用案例分析,我們可以將理論知識(shí)轉(zhuǎn)化為實(shí)際操作,提高問(wèn)題解決能力,隨著科技的不斷發(fā)展,圖形計(jì)數(shù)將在更多領(lǐng)域發(fā)揮重要作用,我們需要不斷學(xué)習(xí)和探索圖形計(jì)數(shù)的最新技術(shù)和應(yīng)用。
“圖形計(jì)數(shù)專題”為我們提供了一個(gè)深入了解圖形結(jié)構(gòu)和性質(zhì)的機(jī)會(huì),通過(guò)掌握相關(guān)概念、應(yīng)用策略和方法以及實(shí)踐案例分析,我們可以更好地應(yīng)用圖形計(jì)數(shù)技術(shù)來(lái)解決實(shí)際問(wèn)題,希望本文能為讀者提供有價(jià)值的見(jiàn)解和指導(dǎo),激發(fā)對(duì)圖形計(jì)數(shù)專題的興趣和熱情。
轉(zhuǎn)載請(qǐng)注明來(lái)自福建光數(shù)數(shù)字技術(shù)有限公司,本文標(biāo)題:《圖形計(jì)數(shù)專題,深度探索與策略解析》













 蜀ICP備2022005971號(hào)-1
蜀ICP備2022005971號(hào)-1
還沒(méi)有評(píng)論,來(lái)說(shuō)兩句吧...